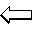
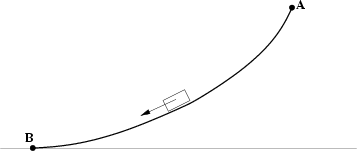
 Propone nel 1696 una sfida che consiste nel trovare la
traiettoria ottimale che deve percorrere una particella per
andare da un punto ad un altro (situato più in basso
ma non direttamente sottostante) nel più breve tempo
possibile.
Tale traiettoria ottimale viene chiamata brachistocrona
Propone nel 1696 una sfida che consiste nel trovare la
traiettoria ottimale che deve percorrere una particella per
andare da un punto ad un altro (situato più in basso
ma non direttamente sottostante) nel più breve tempo
possibile.
Tale traiettoria ottimale viene chiamata brachistocrona
Empiricamente si vede che il segmento che congiunge i due punti non è la soluzione migliore; nemmeno una traiettoria ottenuta con archi di cerchio o con coniche è soddisfacente...
Capita di frequente in matematica di scoprire che problemi apparentemente molto diversi abbiano di fatto la stessa soluzione; a volte ci si accorge di questo anche quando la soluzione stessa non è nota, e ciò è molto comodo per trovare modi alternativi per affrontare il problema.
 Il fiume Brachi Ŕ perfettamente rettilineo ed Ŕ circondato da una
nebbia perenne che si infittisce man mano che ci si avvicina al fiume
In particolare la
visibilitÓ Ŕ legata alla distanza d dal fiume dalla relazione
Il fiume Brachi Ŕ perfettamente rettilineo ed Ŕ circondato da una
nebbia perenne che si infittisce man mano che ci si avvicina al fiume
In particolare la
visibilitÓ Ŕ legata alla distanza d dal fiume dalla relazione
Da un punto A ad una certa distanza dal fiume si vuole raggiungere il punto B posto sul Brachi nel tempo minore possibile tenendo conto che la velocitÓ massima Ŕ direttamente proporzionale alla visibilitÓ.
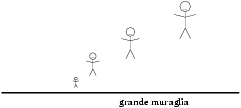 I paesi di Brac e di Bric sono separati da un grande muro.
Solo che in realtÓ non Ŕ il muro che Ŕ grande, quanto gli oggetti che gli
si avvicinano che si rimpiccioliscono man mano.
Il muro magico ha infatti il potere di rimpicciolire gli oggetti di un fattore
I paesi di Brac e di Bric sono separati da un grande muro.
Solo che in realtÓ non Ŕ il muro che Ŕ grande, quanto gli oggetti che gli
si avvicinano che si rimpiccioliscono man mano.
Il muro magico ha infatti il potere di rimpicciolire gli oggetti di un fattore
dove d Ŕ la distanza dal muro. L'effetto per chi gli si avvicina Ŕ come se per lui le distanze si amplificassero di un fattore 1/(k d)1/2. Ci si chiede quale sia il percorso pi¨ corto (geodetica) per raggiungere da A il muro nel punto B; oppure quale sia il percorso pi¨ corto per andare da un punto del muro ad un altro punto del muro.
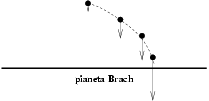 Il pianeta Brach Ŕ molto particolare.
Infatti la sua superficie, che immaginiamo piatta, esercita un campo
gravitazionale il cui potenziale Ŕ:
Il pianeta Brach Ŕ molto particolare.
Infatti la sua superficie, che immaginiamo piatta, esercita un campo
gravitazionale il cui potenziale Ŕ:
e quindi l'accelerazione di gravitÓ Ŕ diretta verso il basso e la componente verticale vale -1/(4h2).
Vogliamo determinare la traiettoria di un sasso lanciato orizzontalmente con una certa velocitÓ iniziale da una certa altezza.
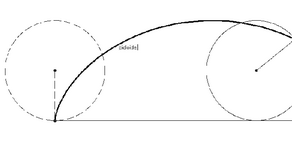 Cerchiamo la curva descritta da un catarifrangente fissato sul cerchione della
ruota di una bicicletta mentre questa si muove (lungo una pista orizzontale
e rettilinea).
Cerchiamo la curva descritta da un catarifrangente fissato sul cerchione della
ruota di una bicicletta mentre questa si muove (lungo una pista orizzontale
e rettilinea).
Questa curva Ŕ nota fin dall'antichitÓ con il nome di cicloide.