 , che è lo stesso 0 in quanto estensibile nella direzione
del positivo (
, che è lo stesso 0 in quanto estensibile nella direzione
del positivo ( =0, come
base dell'estensibilità in positivo di 0).
=0, come
base dell'estensibilità in positivo di 0).
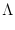 è in realtà un
è in realtà un 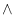 in grassetto e un po'
più grande.
Infine, le formule più semplici sono state ottenute con semplice
testo HTML, ma con l'utilizzo degli elementi <sup> e <sub>
non implementati nelle vecchie versioni dei browser; come controllo la
formula x4 dovrebbe rappresentare "x elevato alla quarta".
(MP)]
in grassetto e un po'
più grande.
Infine, le formule più semplici sono state ottenute con semplice
testo HTML, ma con l'utilizzo degli elementi <sup> e <sub>
non implementati nelle vecchie versioni dei browser; come controllo la
formula x4 dovrebbe rappresentare "x elevato alla quarta".
(MP)]
Osservazione 1. Con l'aggiunta di a (=1), a destra dello 0 e successori, è indefinitamente possibile continuare nella progressione della serie monotona.
Sulla base di
0, a, b, c, n, +, .., ..., ( , ),
da cui
(0+),
(0+a+),
((a+a+)=b+),
((b+a+)=c+), ..,
(n+),
(n+a+), ...,
la serie diviene, però, ripetitiva. Il numero si banalizza. Esso aumenta per semplice ripetizione di (a+), e non c'è spiegamento della serie che sia indipendente dalla comparsa del segno '+' a destra della cifra:
Dalla progressione seriale risulta l'automaticità dell'aggiunta.
Il logicismo (Peano, Russell, Whitehead) spiega la derivabilità della
serie solo per iterazione. I formalisti (Hilbert, Bernays, Weyl,
Kleene), senza più escludere lo zero dalla serie dei numeri naturali
(che scrivono N, omettendo di distinguere fra N0 e
N1), si limitano a raffinare il procedimento derivativo.
Dopo 0, essi scrivono ancora 0, con l'aggiunta dell'apice ', ossia 0',
per indicare l'inerenza (o appartenenza) a zero dell'aumento attribuiti
allo 0. Proprio allo 0, primo numero naturale, quindi non più
estromesso dalla serie dei numeri naturali (nè inclusi in
N0 come numero iniziale della serie dei numeri
zero-inclusivi), appartiene, allora, l'incrementabilità di se stesso.
Ora quel cambiamento di prospettiva concorre alla rifondazione di una teoria generale dei numeri, e, specificatamente, dei numeri relativi.
((0)'), (((0)')'), (((((0)')'..)'..)),
dove l'apice ('..) indica un suo aumento intrafinito, 0,
uguale a se stesso (0=0), richiama  , che è lo stesso 0 in quanto estensibile nella direzione
del positivo (
, che è lo stesso 0 in quanto estensibile nella direzione
del positivo ( =0, come
base dell'estensibilità in positivo di 0).
=0, come
base dell'estensibilità in positivo di 0).
Teorema 1. Diremo (0=0) e (0= ), se (
), se ( =
= ) e (
) e ( =0).
=0).
Con 0,  , 0,
, 0,
 ,
,
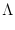 ,
,
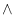 , =,
, =, 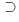 , ( , )
, ( , )
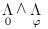 (0=0),
((0=0)
(0=0),
((0=0)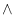 (0=
(0= ))
))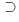 ((
(( =
= )
)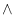 (
( =0))
=0)) 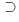
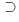 (
( =
= )
)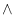 (
( =0),
=0),
(per ogni 0 e  , quando (0=0) e (0=
, quando (0=0) e (0= ), se
(0=0) e (0=
), se
(0=0) e (0= ) implicano (
) implicano ( =
= ) e (
) e ( =0),
allora (
=0),
allora ( =
= ) e (
) e ( =0)).
=0)).
Definizione 1.
Si dirà che 0, con (0=0), esprime il numero k come 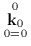 ,
ossia come il numero idem-inclusivo di 0, per cui 0' va solamente verso
il valore assoluto del successore di 0, senza che quest'ultimo sia
estensibile positivamente o negativamente per mezzo di '..,
mentre (0=
,
ossia come il numero idem-inclusivo di 0, per cui 0' va solamente verso
il valore assoluto del successore di 0, senza che quest'ultimo sia
estensibile positivamente o negativamente per mezzo di '..,
mentre (0= ) corrisponde al numero derivato
) corrisponde al numero derivato  -inclusivo
-inclusivo
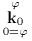 , ossia al numero naturale 0 uguale a
, ossia al numero naturale 0 uguale a  , e va verso la
propria estensibilità in positivo.
, e va verso la
propria estensibilità in positivo.
Teorema 2.
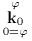 indica il numero naturale derivato 0, però con (0=
indica il numero naturale derivato 0, però con (0= ) e quindi con il passaggio all'incrementabilità di 0.
) e quindi con il passaggio all'incrementabilità di 0.
Infatti, con
k, 0,  , 0,
, 0,  , ',
, ',
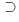 , (, ),
, (, ),
si può scrivere
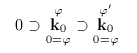
e per il postulato 17 della teoria del numero (Kleene 1952, 82),
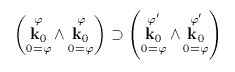 ,
,
derivazione di (a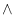 a)
a) 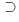 (a'
(a'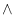 a'), dalla
a'), dalla
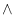 b)
b) 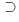 (a'
(a'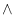 b'),
b'),
che si legge: (a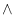 b) implica (a'
b) implica (a'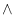 b'),
quando a e b siano aumentati per l'aggiunta di apici (').
b'),
quando a e b siano aumentati per l'aggiunta di apici (').
[...]